What Is Random Fourier Features Method?

Random Fourier features method, or more general random features method is a method to help transform data which are not linearly separable to linearly separable, so that we can use a linear classifier to complete the classification task. For example, in the left illustration, 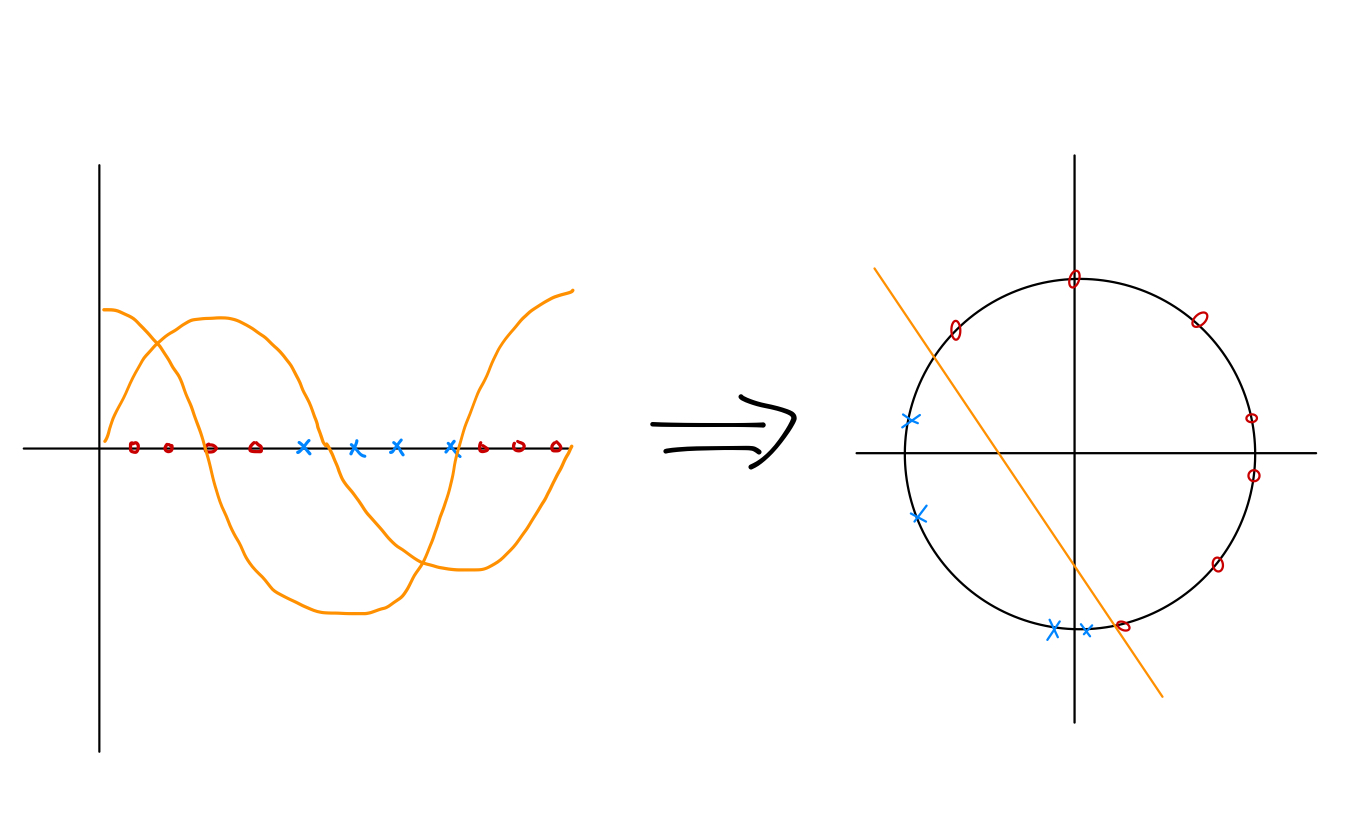the red dots and blue crosses are not linearly separable. By applying the transform

$$\begin{equation} \tilde{x} = \cos(x)\quad\tilde{y} = \cos(x-\pi/2)\,, \end{equation}$$

we get the right illustration and the data are linearly separable. However, in practice, we want to reduce human’s intervention as much as possible, or we do not have much knowledge about what transform is appropriate. So instead of designing specific transform for each task, we just construct the following ones

$$\begin{align} \tilde{x}_1 & = \cos(\gamma\omega_1\cdot x + b_1) \\ \tilde{x}_2 & = \cos(\gamma\omega_2\cdot x + b_2) \\ & \vdots \\ \tilde{x}_N & = \cos(\gamma\omega_N\cdot x + b_N) \\ \end{align}$$

with $\omega_i,b_i$s being randomly selected, usually Gaussian for $\omega$s and uniform in $[0,\pi]$ for $b$s. This is called random Fourier features. There is still a parameter that requires human’s knowledge is the bandwidth parameter $\gamma$. A larger $\gamma$ increases the chance of getting a longer vector dot $x$. Using the illustration above, we can see that too large coefficiens in front of $x$ will wind data points too many rounds and result in points interlacing with each other. If the coefficients are too small, the transform is close to a linear one and does not help (actually in the illustration above, it works, but if we consider the oxox distribution, we will get a trouble). So an appropriate $\gamma$ is crucial for this method to be efficient. Usually it is determined by checking the performance of different $\gamma$s on an validation data set, which is essentially an ugly trial and error.

Another important parameter is the number of features $N$. Theoretically, with sufficiently many features, the training set is always linearly separable. However it may not generalize well to testing set or it costs too much computation resource.

At the end, let’s talk a bit about the history. Using non-linear transform to aid classification and regression has been studied since traditional statistics. Randomly assigning the weights inside the non-linear nodes were also considered after the feedforward network was proposed in 1950s. The appealing part is that it is a convex optimization problem compared to the usual neural networks. In 2007 Rahimi and Recht’s work proposed random Fourier features and pointed out its connection to kernel method. Since then it has attracted more attention. After the revival of deep neural networks, we now know that shallow models like random features plus a linear classifier have disadvantages in representation capability compared to deep models. But it may still provide an efficient method for many problems and a way to understand the generalization performance of neural networks.