Holder’s and Young’s Inequalities

Classical Case

A quick proof of general Holder’s inequality is as follows. First, by Jensen’s inequality, we have for positive $\{a_i\}_{i=1}^n$ and $\{p_i\}_{i=1}^n$ satisfying $\sum 1/p_i = 1$,

$$\begin{align} \prod a_i^{1/p_i} & = \exp\left(\sum\frac{\ln(a_i)}{p_i}\right) \\ & \le \sum \frac{\exp(\ln(a_i))}{p_i} \\ & = \sum\frac{a_i}{p_i}\,. \end{align}$$

Then for functions $\{ f_i \}_1^n$, $L^{p_i}$-integrable, we can set $\vert f_i\vert^{p_i}/\Vert f_i\Vert_{p_i}^{p_i}$ to be $a_i$ and apply the inequality above.

$$\begin{equation} \prod\frac{\vert f_i\vert}{\Vert f_i\Vert_{p_i}} \le \sum\frac{\vert f_i\vert^{p_i}}{p_i\Vert f_i\Vert_{p_i}^{p_i}}\,. \end{equation}$$

Integrate both sides, the general Holder’s inequality gets proved.

Now we prove Young’s convolution inequality (see wikipedia). For $1/p+1/q+1/r=2$ and $f\in L^p,g\in L^q,h\in L^r$, we have

$$\begin{equation} \iint f(x)g(x-y)h(y)dxdy \le \Vert f\Vert_p\Vert g\Vert_q\Vert h\Vert_r\,. \end{equation}$$

Note that $(1-1/p)+(1-1/q)+(1-1/r)=1$, we can apply Holder’s inequality. Set

$$\begin{equation} F(x,y) = [f^p(x)g^q(x-y)]^{1-1/r} \\ G(x,y) = [g^q(x-y)h^r(y)]^{1-1/p} \\ H(x,y) = [h^r(x)f^p(x)]^{1-1/q}\,. \end{equation}$$

Then

$$\begin{align} & \iint f(x)g(x-y)h(y)dxdy \\ & = \iint F(x,y)G(x,y)H(x,y)dxdy \\ & \le \Vert F\Vert_{1-1/r}\Vert G\Vert_{1-1/p} \Vert H\Vert_{1-1/q} \\ & \le \left(\iint \vert f\vert^p \vert g\vert^q\right)^{1-1/r} \left(\iint \vert g\vert^q \vert h\vert^r\right)^{1-1/p} \left(\iint \vert h\vert^r \vert f\vert^p\right)^{1-1/q} \\ & = \Vert f\Vert_p\Vert g\Vert_q\Vert h\Vert_r\,. \end{align}$$

Another form of Young’s inequality is as follows,

$\begin{equation} \Vert f\ast g\Vert_s \le \Vert f\Vert_p \Vert g\Vert_q\,, \end{equation}$ for $1/p+1/q=1+1/s$ and $f,g$ in appropriate spaces. This can be prove by setting $1/s = 1-1/r$ and

$$\begin{equation} h(x) = [f\ast g(x)]^{s-1}\,, \end{equation}$$

and applying the inequality above. Indeed,

$$\begin{align} \Vert f\ast g \Vert_s^s & = \int \left(\int f(y)g(y-x) dy\right)^s dx \\ & = \int \int f(y)g(y-x) dy~h(x)dx \\ & \le \Vert f\Vert_p\Vert g\Vert_q \Vert h\Vert_r\,. \end{align}$$

Note that

$$\begin{align} \Vert h\Vert_r & = \left(\int \vert f\ast g(x)\vert^{r/(r-1)}dx\right)^{1/r}\\ & = \left(\int \vert f\ast g(x)\vert^{s}dx\right)^{1-1/s}\\ & = \Vert f\ast g\Vert_s^{s-1}\,. \end{align}$$

The proof is complete.

Note that the derivation above can be simplified using the dual space argument. For $s$ satisfying $1/s+1/r=1$,

$$\begin{align} \Vert f\ast g\Vert_s & = \sup_{\Vert h\Vert_r\le 1} \int (f\ast g)(x)h(x) dx \\ & \le \sup_{\Vert h\Vert_r\le 1} \Vert f\Vert_p\Vert g\Vert_q \Vert h\Vert_r \\ & = \Vert f\Vert_p\Vert g\Vert_q\,. \end{align}$$

Vector Case

When $\vec{f}=(f_1,\ldots,f_n)$ is a vector valued map, the convolution with a scalar function $g$ can be defined by component-wise convolution. The output of the convolution is still an $n$-vector valued function. Its $(2,r)$-norm is defined by

$$\begin{equation} \left(\int\Vert \vec{f}\ast g(x)\Vert_2^r dx\right)^{1/r}\,. \end{equation}$$

We can show that it still satisfies Young’s inequality.

$$\begin{align} \Vert\vec{f}\ast g\Vert_{2,r} & = \left\Vert\Vert \vec{f}\ast g(x)\Vert_2\right\Vert_r\\ & = \left\Vert\sup_{\vec{v}\in S^{n-1}} \vec{f}\ast g(x) \cdot v\right\Vert_r \\ & \le \left\Vert\sup_{\vec{v}\in S^{n-1}} \int\vert\vec{f}(t)\cdot v\vert \vert g(t-x)\vert dt \right\Vert_r \\ & \le \left\Vert \Vert\vec{f}\Vert_2\ast \vert g\vert\right\Vert_r \\ & \le \Vert\vec{f}\Vert_{2,p}\Vert g\Vert_q\,. \end{align}$$

Reverse Case

All the results above hold for $1\le p,q,r$. Actually, for $0\le p,q,r\le 1$, we have the reverse Holder’s and Young’s inequality. We start with reverse Jensen’s inequality. Note that for a convex function $f$ and $\{x_i\}_{i=1}^n$ in its domain, we always have

$$\begin{equation} f\left(\sum c_i x_i\right) \begin{cases} \le \sum c_if(x_i)\quad & \sum c_i = 1\wedge \forall i ~c_i\in [0,1]\,,\\ \ge \sum c_if(x_i)\quad & \sum c_i = 1\wedge \forall i\ne k ~c_i\le 0,c_k\ge 1\,. \end{cases} \end{equation}$$

The second case describes the case when the affine combination of $\{x_i\}$ is outside a corner of the convex hull. The 1-dim case is shown below,

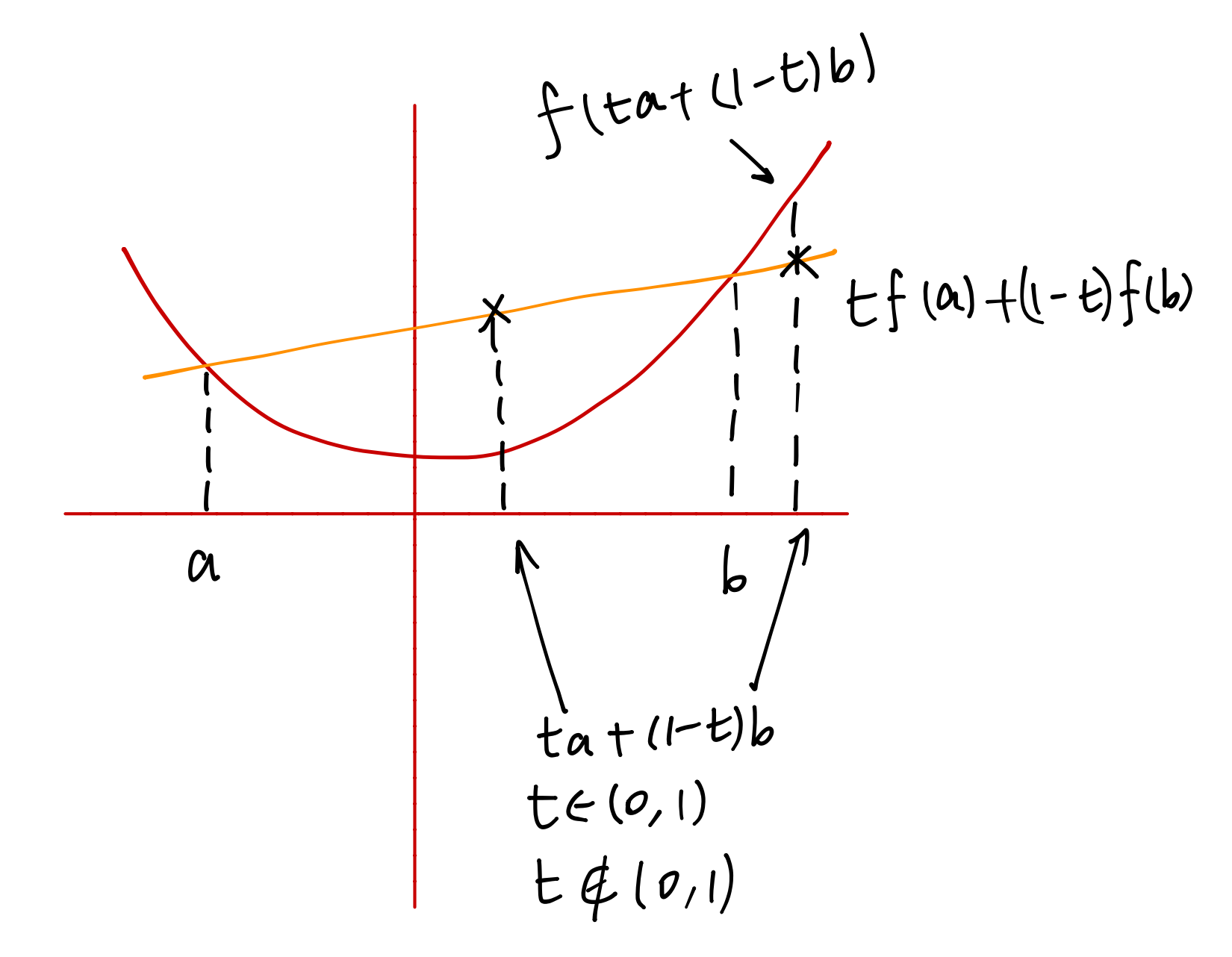
The proof of the second case is based on the first case. Denote $x_0 = \sum c_i x_i$. Since $c_k\ge 1$ we have

$$\begin{equation} c_k = 1 - \sum_{i\ne k}c_i\\ 1 = \frac{1}{c_k}+\sum_{i\ne k}\frac{-c_i}{c_k}\\ x_k = \frac{x_0}{c_k}+\sum_{i\ne k}\frac{-c_ix_i}{c_k}\,. \end{equation}$$

By usual Jensen’s inequality, we have

$$\begin{equation} f(x_k) \le \frac{f(x_0)}{c_k} + \sum_{i\ne k} \frac{-c_i f(x_i)}{c_k}\\ f(x_0) \ge \sum_{i}c_if(x_i)\,. \end{equation}$$

The general case, that is for more than 1 coefficients greater than $1$, does not hold. It can be shown by the following illustration.

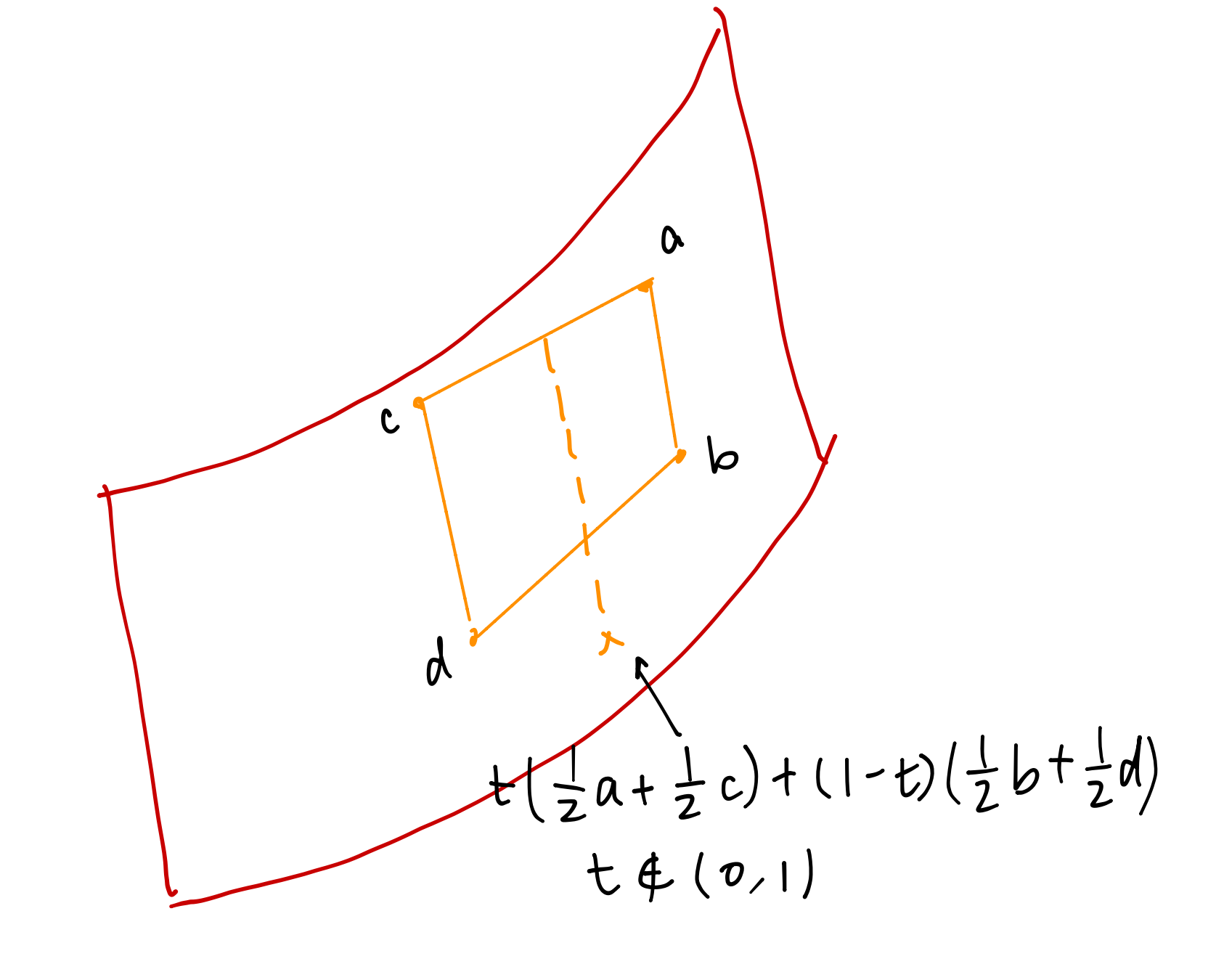
When $t$ is sufficiently large, the coefficients of $a,c$ are greater than $1$ and the ones of $b,d$ are less than $0$. But since the dashed line is always parallel and above the surface,

$$\begin{equation} f\left(\frac{ta+tc+(1-t)b+(1-t)d}{2}\right) \\ \le \frac{tf(a)+tf(c)+(1-t)f(b)+(1-t)f(d)}{2}\,. \end{equation}$$

By reverse Jensen’s inequality, we have for $a,b,c > 0$, $p,q\le 0, s\ge 1$, and $p+q+s=1$,

$$\begin{equation} a^pb^qc^s \ge \frac{a}{p}+\frac{b}{q}+\frac{c}{s}\,. \end{equation}$$

Then reverse Holder is given by

$$\begin{equation} \Vert fgh\Vert_1 \ge \Vert f\Vert_p\Vert g\Vert_q\Vert h\Vert_s\,, \end{equation}$$

for $1/p+1/q+1/s=1, p,q<0,s<1$. Clearly we need $f,g$ to be almost surely non-zero. $\Vert\cdot\Vert_{p/q/s}$ are just convenient notations, not norms.

Repeat the argument for the classical case, we get the reverse Young’s inequality,

$$\begin{equation} \Vert f\ast g\Vert_r \ge \Vert f\Vert_q\Vert g\Vert_q\,, \end{equation}$$

for $1/p+1/q=1+1/r, 0<p,q,r<1$.